numpy.fft模块本来用于计算傅立叶变换,和傅立叶级数有关系但不是一回事。对于周期为$T$的实函数,如果我们能够获得其一个周期的函数值,实际上也是可以使用numpy.fft做傅立叶展开的。
叠加cos函数的傅立叶展开
我们输入一个np.array作为一个周期内的函数值,函数值都是实数。如果这个函数能够完全使用$\cos$函数展开而不涉及$\sin$函数,那么我们希望得到的傅立叶级数系数数组也应该是实数组。所以此对称性可以使用numpy.fft.hfft加以利用。hfft返回一个实数列$H_k$,其图像为一些峰,这些峰的横坐标$k$与这些峰的角频率$\omega$的关系是
峰高$H$与$\cos$函数振幅$A$的关系为
这里$N$为输入的函数值数组的长度。
以下我们通过一些测试说明怎么使用。
我们先通过一个例子解释、验证上面的公式,从表现上知道hfft的作用效果。我们给出一个已知傅立叶展开系数的函数
通过傅立叶级数展开,我们希望得到各个展开$\cos$函数的角频率以及幅度。
首先导入numpy包1
import numpy as np
我们的输入是1
2
3
4
5
6
7N = 500
x = np.linspace(0,6,N)
omega1 = 5 * np.pi
omega2 = 3 * np.pi
omega3 = 2 * np.pi
omega4 = 1 * np.pi
y = 3*np.cos(omega1*x) + 5*np.cos(omega2*x) + 7*np.cos(omega3*x) + 2*np.cos(omega4*x)
这里linspace参数6来自于y函数的一个周期$T=6$。做傅立叶展开
1 | z = np.fft.hfft(y)/(N-1) |
得到z是一个实数列。画出图可以看到有八个尖峰,整个图像是对称的。我们只取其前一半即可,因为后一半是傅立叶变换本身产生的对称图像。图像四个峰分别在$k=6,12,18,30$。注意$T=6$。使用上面的公式可得到$\omega=\pi,2\pi,3\pi,5\pi$,与我们期望的一致。其峰高依次为$A=2,7,5,3$,与角频率完全一一对应。
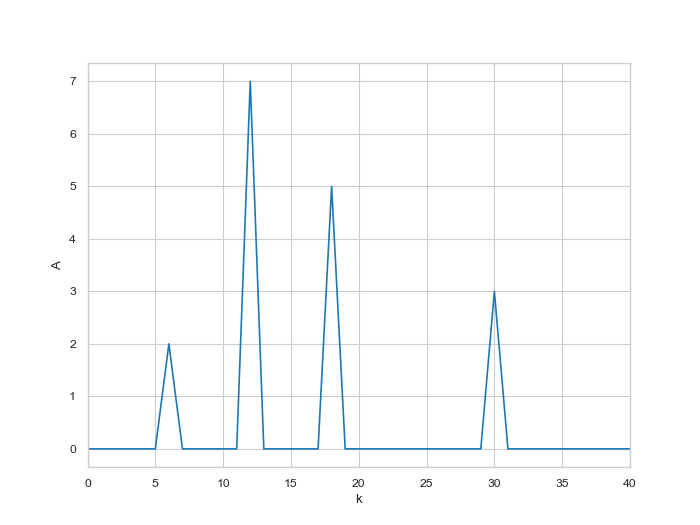
注意:改变N值不会影响傅立叶展开,只要够大就可以了。
此外,假如我们给出的y数组为两个周期,那么只要令$T$等于两倍原来周期,最后的结果$\omega,A$不会变,与我们期望的一致。
叠加cos和sin函数的傅立叶展开
一个函数完整的傅立叶展开可能包含$\sin$项,在傅立叶变换后其幅度值被分到了虚数部分,此时我们应当使用numpy.fft.fft来展开,得到一列复数。我们输入一个np.array作为一个周期内的函数值,函数值仍然都是实数。fft返回一个复数列$H_k$,对其实部和虚部分别作图,其图像为一些峰,这些峰的横坐标$k$与这些峰的角频率$\omega$的关系是
复数峰高$H$与$\cos$函数振幅$A$的关系为
复数峰高$H$与$\sin$函数振幅$B$的关系为
这里$N$为输入的函数值数组的长度。$\Re,\Im$分别为取实部、虚部。
以下我们通过一些测试说明fft怎么使用。我们给出一个已知傅立叶展开系数的函数
通过傅立叶级数展开,我们希望得到各个展开$\cos$和$\sin$函数的角频率以及幅度。
首先导入numpy包1
import numpy as np
我们的输入是1
2
3
4
5
6
7N = 500
x = np.linspace(0,6,N)
omega1 = 5 * np.pi
omega2 = 3 * np.pi
omega3 = 2 * np.pi
omega4 = 1 * np.pi
y = 3*np.sin(omega1*x) + 5*np.cos(omega2*x) + 7*np.cos(omega3*x) - 2*np.sin(omega4*x)
这里linspace参数6来自于y函数的一个周期$T=6$。做傅立叶展开
1 | z = np.fft.fft(y)/N*2 |
得到z是一个复数列,我们仍旧只取其前一半。其实部z.real图像有两个主要的峰,分别在$k=6,9$,对应角频率为$\omega=2\pi,3\pi$、幅度为$A=7,5$的两个$\cos$函数;其虚部相反数-z.imag图像也有两个主要的峰,分别在$k=3,15$,对应角频率为$\omega=\pi,5\pi$、幅度为$B=-2,3$的两个$\sin$函数。以上结果与我们期望的一致。
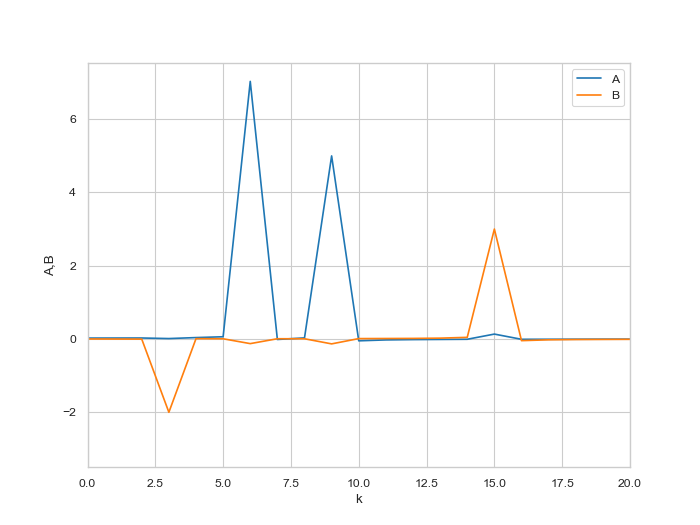
注意,以上使用fft得到的峰值并非严格等于我们期望的数值;而用之前hfft在纯$\cos$的情况下可以得到精确的峰值。