量子散射理论用于解决粒子碰撞等量子力学过程，主要解法有分波法和Born近似方法。本文介绍这两种计算方法，并且展示其基本原理。

基本概念

散射中心 靶粒子所在的位置成为散射中心。采用质心系研究散射问题时，散射中心为坐标原点；在质心系中入射粒子的质量以约化质量$\mu$表示。
散射角 $(\theta,\phi)$ 入射粒子受靶粒子势场作用，其运动方向偏离入射方向的角度。
弹性散射 指散射过程中，入射粒子和靶粒子内部状态都不发生变化。
粒子流密度 $\bm{J}$ 单位时间内垂直通过单位面积的粒子数。用于描述入射粒子流的强度。

量子力学中，粒子流密度的计算公式为

$\bm{J}=\frac{\hbar}{\mu}\mathrm{Im}(\psi^+\nabla\psi)$

散射截面

微分散射截面 $\dfrac{d\sigma}{d\Omega}(\theta,\phi)$ 粒子散射到$(\theta,\phi)$方向的概率。

若已知入射流密度$\bm{J}_i$和散射流密度$\bm{J}_s(\theta,\phi)$，则

$\begin{equation}\label{eqn1} \frac{d\sigma}{d\Omega}(\theta,\phi)=\frac{r^2J_s(\theta,\phi)}{J_i} \end{equation}$

（总）散射截面 $\sigma=\int\dfrac{d\sigma}{d\Omega}(\theta,\phi)d\Omega$

散射截面具有面积的量纲。

量子力学的任务是从理论上计算微分散射截面$\frac{d\sigma}{d\Omega}(\theta,\phi)$。散射截面与粒子间相互作用（即靶粒子势场）有直接关系。

散射幅：量子力学求散射截面

通常将散射问题的定态Schrödinger方程写为

$\begin{equation} \nabla^2\psi+[k^2-V(r)]\psi=0 \end{equation}$

导出过程

由
$-\frac{\hbar^2}{2\mu}\nabla^2\psi+U(r)\psi=E\psi$
令$k^2=\frac{2\mu E}{\hbar^2}$，$V(r)=\frac{2\mu}{\hbar^2}U(r)$即可。这里$\frac{\hbar k}{\mu}$可以理解为粒子的相对速度。通常散射问题给定能量，也就是给定了初始动能，也就给定了粒子入射速度。这样，k就是方程中的一个常数。

注意散射问题中的势通常为中心势。取球极坐标时，通常设粒子入射方向为极轴。

该方程的通解在$r\to\infty$时的渐近形式为应为入射平面波与散射球面波的叠加，

$\begin{equation}\label{eqn3} \psi(\bm{r})\sim Ae^{i\bm{k}\cdot\bm{r}} + Af(\theta,\phi)\frac{e^{ikr}}{r} \end{equation}$

式中 $f(\theta,\phi)$ 可以看做球面波的角向概率分布，称为散射幅。散射幅与散射截面有直接的联系：

$\begin{equation} \frac{d\sigma}{d\Omega}(\theta,\phi)=|f(\theta,\phi)|^2 \end{equation}$

导出过程

由式$\eqref{eqn3}$中入射与散射波函数可求得入射与散射流密度的径向分量分别为
$J_i=|A|^2\frac{\hbar k}{\mu},\qquad J_s=|A|^2\frac{\hbar k}{\mu}\frac{|f(\theta,\phi)|^2}{r^2}$
由式$\eqref{eqn1}$即可得到微分散射截面。

只要给定靶粒子势$V(r)$，通过解薛定谔方程并取$\psi(\bm{r})$在$r\to\infty$的渐近形式就可以得到$f(\theta,\phi)$。因此$f(\theta,\phi)$是连接量子力学理论和实验数据的关键，因此量子散射理论的核心是寻找求解散射幅$f(\theta,\phi)$的各种方法。其中分波法和Born近似是两种常用方法。

分波法

分波法的核心思想是在球谐函数（或Legendre多项式）展开下求波函数的级数解。这一方法将求散射幅$f(\theta,\phi)$的问题归结为求分波的相移$\delta_l$，而$\delta_l$需要通过势函数$V(r)$的具体情况求解径向方程来获得。

分波法计算方法

确定精确到前多少个分波
粒子波数为$k=\sqrt{\frac{2\mu E}{\hbar^2}}$，势场作用范围为$r=a$，则可以精确到$0\leqslant l< ka$。在极慢速近似也可以只计算s分波（$l=0$)。
解径向方程
$\frac{d^2u_l}{dr^2}+\left[k^2-V(r)-\frac{l(l+1)}{r^2}\right]u_l(r)=0$
其中$V(r)=\frac{2\mu U(r)}{\hbar^2}$，$U(r)$为势能。
解得$u_l$为正弦函数或者Bessel函数等，后者取$r\to\infty$渐进形式得到正弦函数。
求相移
将渐进解的相写为$\left(kr-\frac\pi2l+\delta_l\right)$的形式，得到相移$\delta_l$。
求散射截面
微分散射截面
$\frac{d\sigma}{d\Omega}(\theta)=|f(\theta)|^2=\left|\frac1k\sum_l(2l+1)P_l(\cos\theta)e^{i\delta_l}\sin\delta_l\right|^2$
第$l$个分波的散射截面为
$\sigma_l=\frac{4\pi}{k^2}(2l+1)\sin^2\delta_l$
总散射截面为$\sigma=\sum_l\sigma_l$

分波法原理

由于波动方程$\eqref{eqn1}$在球极坐标下有通解

$\begin{equation}\label{eqn5} \psi(r,\theta)=\sum_lR_l(r)P_l(\cos\theta) \end{equation}$

其中$R(r)$为待求的径向波函数。通解中每个特解称为一个分波，$R_l(r)P_l(\cos\theta)$称为第$l$个分波，通常称$l=0,1,2,3,…$的分波分别为s,p,d,f,…分波。

径向波函数$R_l(r)$的$r\to\infty$的渐进解为

$\begin{equation}\label{eqn6} R_l(r)\sim\frac{A_l}{kr}\sin\left(kr-\frac\pi2l+\delta_l\right) \end{equation}$

导出过程

将通解$\eqref{eqn5}$代入波动方程$\eqref{eqn1}$得到径向方程
$\frac1{r^2}\frac{d}{dr}\left(r^2\frac{dR_l}{dr}\right)+\left[k^2-V(r)-\frac{l(l+1)}{r^2}\right]R_l(r)=0$
令 $R_l(r)=\frac{u_l(r)}r$，得到
$\frac{d^2u_l}{dr^2}+\left[k^2-V(r)-\frac{l(l+1)}{r^2}\right]u_l(r)=0$
若已知$V(r)$，则可求解此方程得到最终解。此处我们讨论一般情况。

考虑方程在$r\to\infty$下的渐近形式，要求$V(r)\to 0$，
$\frac{d^2u_l(r)}{dr^2}+k^2u_l(r)=0$
得到渐近解（调整系数后）
$u_l(r)=\frac{A_l}{k}\sin\left(kr+\delta_l-\frac{\pi}2l\right)$
最终得到径向分布函数的渐近解$\eqref{eqn6}$。

需要注意的是$A_l$和$\delta_l$的来源不一样。$A_l$可以看做通解中特解的系数，而$\delta_l$的未知来源于势函数$V(r)$性质的不明确，少了一个$r=a<\infty$处的边界条件。所以我们应当将$\delta_l$先看做参数，通过$r\to\infty$处的边界条件求解$A_l$和$f(\theta)$。

将正弦函数改写为幂函数和形式并代入$\eqref{eqn5}$，得到波函数的渐近解为

$\begin{equation}\label{eqn7} \psi(r,\theta)\sim\sum_l\frac{A_l}{2ikr}\left[e^{i(kr-\pi l/2+\delta_l)}-e^{-i(kr-\pi l/2+\delta_l)}\right]P_l(\cos\theta) \end{equation}$

其中，$P_l(\cos\theta)$为Legendre多项式；而$A_l$与$\delta_l$需要根据边界条件$\eqref{eqn3}$求。

边界条件$\eqref{eqn3}$中平面波按球面波展开，最终得到

$\begin{equation}\label{eqn8} \psi(r,\theta)\sim f(\theta)\frac{e^{ikr}}r+\sum_l\frac{(2l+1)i^l}{2ikr}\left[e^{i(kr-\pi l/2)}-e^{-i(kr-\pi l/2)}\right]P_l(\cos\theta) \end{equation}$

导出过程

将平面波$e^{ikz}$按球面波展开
$e^{ikz}=e^{ikr\cos\theta}=\sum_l(2l+1)i^lj_l(kr)P_l(\cos\theta)$
其中$j_l(kr)$是球Bessel函数，在$r\to\infty$下的渐近形式为
$j_l(kr)\to\frac1{kr}\sin\left(kr-\frac{\pi}2l\right)=\frac1{2ikr}\left[e^{i(kr-\pi l/2)}-e^{-i(kr-\pi l/2)}\right]$
代入式$\eqref{eqn3}$即可得到$\eqref{eqn8}$。

利用$e^{ikr}$与$e^{-ikr}$的正交性以及Legendre多项式的正交性，得到

$\begin{gather} A_l=(2l+1)\exp\left[i\left(\frac{\pi}2l+\delta_l\right)\right]\label{eqn9}\newline f(\theta)=\frac1k\sum_l(2l+1)e^{i\delta_l}\sin\delta_lP_l(\cos\theta)\label{eqn10} \end{gather}$

导出过程

式$\eqref{eqn7}$和$\eqref{eqn8}$中$e^{ikr}$和$e^{-ikr}$系数分别相等，得到两个方程
$\begin{gather}\sum_lA_le^{(\delta_l-l\pi/2)}P_l(\cos\theta)=2ikf(\theta)+\sum_l(2l+1)i^le^{-il\pi/2}P_l(\cos\theta)\nonumber\newline \sum_lA_le^{-(\delta_l-l\pi/2)}P_l(\cos\theta)=\sum_l(2l+1)i^le^{il\pi/2}P_l(\cos\theta)\nonumber \end{gather}$
第二式利用Legendre函数正交性，两边乘$P_{l’}(\cos\theta)$并积分就得到
$A_le^{-i(\delta_l-\pi l/2)}=(2l+1)i^le^{i\pi l/2}$
即式$\eqref{eqn9}$。

最终，得到微分散射截面

$\begin{equation} \frac{d\sigma}{d\Omega}(\theta)=|f(\theta)|^2=\left|\frac1k\sum_l(2l+1)P_l(\cos\theta)e^{i\delta_l}\sin\delta_l\right|^2 \end{equation}$

以及总散射截面

$\begin{equation} \sigma=2\pi\int\frac{d\sigma}{d\Omega}(\theta)\sin\theta d\theta=\frac{4\pi}k^2\sum_l(2l+1)\sin^2\delta_l \end{equation}$

若将散射截面写为$\sigma=\sum_l\sigma_l$，则

$\begin{equation} \sigma_l=\frac{4\pi}{k^2}(2l+1)\sin^2\delta_l \end{equation}$

为第$l$个分波的散射截面。

关于相移

由入射波和散射波的形式可知，

$\left(kr-\frac\pi2l\right)$是入射波第$l$个分波的相
$\left(kr-\frac\pi2l+\delta_l\right)$是散射波第$l$个分波的相
所以$\delta_l$是入射波经散射后第$l$个分波的相移。

求相移$\delta_l$需要知道一个$r=a<\infty$处的边界条件。由于靠近原点（靶粒子），需要知道具体的势函数。

分波法的适用性

球Bessel函数

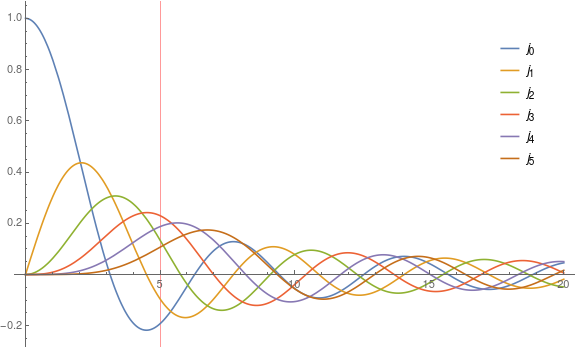
由于入射波的第$l$个分波的径向函数$j_l(kr)$第一极大值位于$r=\frac{l}k$附近，并随$r$增大衰减到0，若$j_l(kr)$的第一极大值位于$r=\frac{l}k>a$（这里$a$表示势函数的作用范围），那么在势函数作用范围内$j_l(kr)$的值就很小，意味着第$l$个分波受势场的影响可以忽略。所以可以忽略的$l$为$l>ka$，这里$k$是能量的函数。粒子能量越低，影响显著的分波数量就越少。所以分波法非常适用于低能（长波）极限下，截取的分波只要$l< ka$即可，极慢速粒子甚至可以只考虑s分波。

Born近似

Born近似的核心思想是微扰论。当入射粒子能量较高时，不宜使用分波法；此时势能可以看作自由粒子Hamilton量的微扰。

Born近似计算方法

Born近似表达式为

$\begin{equation} \frac{d\sigma}{d\Omega}(\theta,\phi)=\frac{4\mu^2}{K^2\hbar^4}\left|\int_0^\infty rU(r)\sin(Kr)dr\right|^2 \end{equation}$

其中 $ K=2k\sin\frac{\theta}2$，$\theta$为散射角。

常见复杂作用势能$U(r)$及对应积分$\int_0^\infty rU(r)\sin(Kr)dr$

$e^{-ar}\to$ $\int_0^\infty re^{-ar}sin(Kr)dr=\frac{2aK}{(a^2+K^2)^2}$
$e^{-a^2r^2}\to$ $\int_0^\infty re^{-a^2r^2}\sin(Kr)dr=\frac{\sqrt{\pi}Ke^{-K^2}{4a^2}}{4a^3}$
$\frac{e^{-ar}}r\to$ $\int_0^\infty e^{-ar}\sin(Kr)dr=\frac{K}{a^2+K^2}$
$\frac1{r^2}\to$ $\int_0^\infty\frac{\sin Kr}rdr=\frac{\pi}2$

量子散射理论