量子力学中角动量的合成
- 角动量算符$\brm{J}_1,\brm{J}_2$各自的本征态为$|j_1m_1\ra,|j_2m_2\ra$,则其直积态为$|j_1m_1j_2m_2\ra$。
- 角动量算符通过加法可以定义新角动量算符:$\brm{J}=\brm{J}_1+\brm{J}_2$,其本征态为$|jm\ra$,在直积空间中表示为$|j_1j_2jm\ra$。
- $|j_1m_1j_2m_2\ra$和$|j_1j_2jm\ra$为线性无关的两组基。Clebsch-Gordan系数(CG系数)是这两组基之间的变换矩阵,也就是说一组基在另一组基下的展开系数。
本文Clebsch-Gordan系数(CG系数)记号为$\la j_1m_1j_2m_2|jm\ra$。若有负号则写在数字上方。
Clebsch-Gordan系数计算步骤
参数取值范围
在计算某一CG系数之前,首先判断其是否为零,了解该CG系数在图像中所处的位置。
- 通常,$j_1,j_2\geqslant0$是给定值,可以取整数或者半整数。$j_1,j_2$是两组基共有的量子数,也就是说基组变换前后$j_1,j_2$不变。这也是记号中合成基一侧可以省略$j_1,j_2$的原因。
- $m_1,m_2$的取值为$0,\pm 1,…,\pm j_1,0,\pm 1,…,\pm j_2$。
- $j$的取值范围为$|j_1-j_2|,|j_1-j_2|+1,…,j_1+j_2$。
- $m$的取值只能为$m=m_1+m_2$且不能超出$\pm j$的范围。
不满足此参数条件的CG系数都为零。
参数取值范围的图像
给定$j_1,j_2$后,可取的$(m_1,m_2)$构成了一个二维的矩形点阵。由于必有$m=m_1+m_2$,所以每一个点对应的$m$也是确定的。$m$值相同的点在同一条斜率为$-1$的直线上。
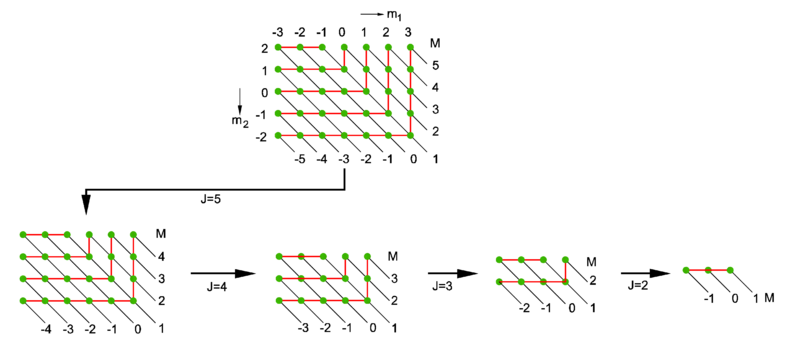
CG系数为1的点:Condon–Shortley约定
约定$\la j_1j_1j_2j_2|jj\ra=1,\quad j=j_1+j_2$。这一点位于图像的右上角。这一点通常为CG系数迭代计算的起点。
原因因为$|m_1=j_1,m_2=j_2\ra$必须等于$|j=j_1+j_2,m=j_1+j_2\ra$,除了一个任意的相因子。这个相因子就被约定为1。
CG系数的迭代关系
使用升降算符可以得出CG系数的迭代关系
$J_+$对应的系数为$\sqrt{(j-m)(j+m+1)}$,$J_-$对应的系数为$\sqrt{(j+m)(j-m+1)}$。
$j$ 取最大值时的计算
利用迭代关系式$\eqref{eqn:2}$,从图像的右上角开始逐步计算$j=j_1+j_2$时不同$m_1,m_2$对应的CG系数。
通常将已知的点代入式$\eqref{eqn:2}$的右侧,待求的点放在左侧。在图像中,上边缘的点只依赖于其右邻点,右边缘的点只依赖与其上邻点,中间的点则依赖于右邻点和上邻点。
$j$ 取最大值减一时的计算
$j=j_1+j_2-1$时,$m$的可取的范围在图像上缩小,即不再包含$m=\pm(j_1+j_2)$两个点。此时不能立刻使用CG系数为1的点,必须经过转化。
首先,计算$m$取最大值$j_1+j_2-1$。此时可以列出基组的变换:
这两个矢量正交;其中$A_{ij}$都是CG系数,并且其中第一行的$A_{11},A_{12}$都是已知的。这样通过解方程可以得出第二行的$A_{21},A_{22}$。在归一化后,仍然有一个相因子的自由度,这个自由度由Condon-Shortley约定消除:规定$m$取最大值$j$、$m_1$取最大值$j_1$时的CG系数为正实数。这里即规定$A_{21}>0$。这样CG系数都为确定值。
在确定右上角两个值之后,再利用迭代关系可以求出$j=j_1+j_2-1$时其他的CG系数。
$j$ 取一般非最大值时的计算
类比取最大值减一的方法,只是要列出三个、四个或更多的基组变换等式来求解,因为右上角斜边缘的点变成了三个、四个或更多。同时,相因子使用Condon-Shortley约定决定即可。
使用程序计算CG系数
如Mathematica,SymPy等。
参考资料
- Sakurai & Napolitano, Modern quantum mechanics (1994)
- Citizendium, Angular momentum coupling