Ising模型是统计物理学最经典的模型之一,由Wilhelm Lenz在1920年提出。Ising模型属于点阵模型,最初被设计用于描述铁磁性相变,现在已经在各个领域都有广泛应用。其模拟技术简单、典型。
定义
一个点阵系统的每个格点$i$有一个离散随机变量$s_i$,其值为$\pm 1$。这个变量在描述磁现象的问题中,即为格点的自旋。当每一个格点$i$都指定了确定的$s_i$,这样集合$s=\\{s_i\\}$就是系统的一个组态。这样的描述是许多点阵模型共有的。
Ising模型的核心是其哈密顿量:对于组态$s=\\{s_i\\}$,
其中$\la ij\ra$是通用的记号,表示所有最近邻的格点$i,j$对。$J_{ij}$描述最近邻格点的相互作用,$h_i$描述外场作用。
相互作用参数$J_{ij}$
$J_{ij}>0$,则该系统为铁磁性(Ferromanetism, FM),相邻格点倾向于同号(自旋平行)
$J_{ij}< 0$,则该系统为反铁磁性(Antiferromagnetism, AFM),相邻格点倾向于反号(自旋反平行)
$J_{ij}=0$,表示自旋间无相互作用。
除此之外该系统为非铁磁性。
Ising模型通常指铁磁性体系$J_{ij}>0$。而且为了研究其最本质的性质,会假设所有的$J_{ij}$都相等。
外场参数$h_{i}$
描述外场和格点之间的相互作用。格点顷向于和外场$h_i$同号(同向)。
通常以二维正方晶格作为图形示例:
通常讨论的Ising模型是所有$J_{ij}$相等$J_{ij}=1$(取为能量单位),所有$h_i$相等$h_i=h$的立方格子模型。其他衍生的Ising模型有变更点阵(三角、六角、四方等)、变更相互作用强度$J_{ij}$的选择(反铁磁、随机键自旋玻璃等)、变更外场$h_i$(随机场、周期场等)以及增加长程相互作用(Ising-Coulomb模型)等。这些广义Ising模型往往需要做专门讨论,不在此文的讨论范围内。
性质与现象
温度$T$
在零温下,系统的组态取能量最低态(基态),所有的物理学性质由基态决定。但是温度非零时,系统的物理学性质由所有组态性质的Boltzmann加权平均求得。这是对Ising模型进行Monte Carlo模拟的出发点。各组态的权重即Boltzmann分布,
这里$\beta=\frac{1}{k_BT}$是常用的温度记号。能量(哈密顿量)越低的组态权重越大(这也就是上面“倾向于”的具体含义)。
模拟时,Ising模型的温度$T$一般是事先给定的。
待求的物理量
通常统计的物理量包括:
能量(系统总能量)
热容(单位粒子热容)
磁矩(系统总磁矩)
无外场时,统计上的磁矩应当恒为零。实际铁磁体在居里温度(临界温度)之下存在非零磁矩,是因为对称性自发破缺,称为自发的宏观磁矩。若希望计算这一性质不妨统计磁矩的模长$|M(s)|$。
平均磁矩(单位粒子磁矩)记为
磁化率(单位粒子磁化率)
磁化率的定义在各种文献中形式不一,主要区别是在是否除以一个温度。一般物理、化学教材(如费曼物理学第二卷[6],IUPAC Gold Book[7],Baxter可解模型[8],Pathria统计力学教材[4]等)定义(单位)磁化率magnetic susceptibility为
Chandler的统计力学教材[9]第五章定义susceptibility为
看上去前一种定义更准确、更常用。本文后面的磁导率都以前一种定义方法定义。
高于临界温度$T_c$时,磁化率应当为0。低于临界温度时,由于对称性自发破缺,磁矩不为零。临界温度相当于铁磁体的居里温度。
关联强度与特征尺度
关联强度定义为
远离相变温度时,关联强度呈现指数衰减:
这里$r_0$为一常数。在接近相变温度时,$r_0$不再是一个常数,而呈现出温度的幂律行为,见下文。
重要的现象
二级相变
在无外场的情况下,二维及以上铁磁Ising模型存在二级相变温度$T_c$,即能量、磁矩随温度连续,热容、磁化率随温度不连续。高温时为顺磁态,低温时为铁磁态。
在临界点,系统具有长程关联性质,组态呈现出自相似的特点。这是Ising模型的重正化方法的出发点。
一维Ising链不存在相变。简单二维Ising模型在无穷尺寸晶格下的临界温度$k_BT_c/J=\frac{2}{\ln(1+\sqrt{2})}\approx 2.27$。简单三维Ising模型临界温度$k_BT_c/J\approx 4.512$。
对称性自发破缺
无外场的Ising模型的哈密顿量具有$Z_2$对称性,即在统计中将组态中的$+1$改成$-1$,$-1$改成$+1$,统计结果不变(最多差一个符号,比如磁矩),也就是说这两个组态简并。在低温时,系统接近简并的基态(全部+1或全部-1),热力学过程中最终只能选择一个。这种物理现象就是对称性自发破缺。
从动力学的角度来看,两个基态之间的势垒非常高,以至于低温下的涨落难以克服,所以系统不会在两个基态之间来回快速转换。与之对比,高温下涨落比较大,出现大块相同符号格点的“团簇”的情况比较少,系统能够比较快地达到平衡。
因此,在模拟中,低温情况下需要考虑如何克服势垒的影响以满足遍历性要求。见下文Wolff Cluster算法。
尺寸效应
相变不可避免地涉及到尺寸效应。临界温度会随着体系的增大而趋近一个定值。二维时最简单二维正方晶格Ising模型的临界温度$T_c\approx2.26918531$。
幂律行为与临界指数
在相变点附近,Ising模型的物理量出现随温度、外场的幂律行为,即
这里$h$是外场,$d$是维度。前三式表示在零外场下,第四式表示在临界温度下。幂指数$\alpha,\beta,\gamma,\delta,\nu,\eta$称为临界指数,其数值大小在同一维度下与系统的尺寸无关。求不同维度下临界指数数值一度是Ising模型理论和模拟的研究热点。从Ising、Onsager到杨振宁、李政道,都曾经对该领域做出详细的研究。
更详细的定义说明参见[4]第12章8节、12节。
计算设定
约化单位
计算机模拟只能直接给出一个数字,而不能给出一个带单位的物理值。在计算中我们需要设定单位以使得输入输出的纯数字有意义。这里设定单位并不是指具体的设定米还是英尺这样的单位,而是找基准的物理参数作为数字的单位,或者说得到的数字最终被理解为基准物理参数的多少倍。
例如,在Ising模型中,我们选择参数$J$作为能量的单位。$J$本身就是一个有着能量单位的物理量,这样我们在计算中得出的任何应该具有能量单位的物理量的数字,只要乘上给定的$J$,也就换算成了真实体系的数字,可以与实际物理量进行比较。因此,$J$本身也决定了体系能量的尺度。尺度的变化不应当导致程序运算结果的变化。
这里我们选择$J$为能量单位,那么温度$\beta$的单位就是$J^{-1}$,温度$T$的单位就是$J\cdot k_B^{-1}$。平均热容的物理量的单位就是$k_B$。显然,$J$的具体取值不会影响到约去单位以后的物理量的计算结果。此时系统的哈密顿量写为
此式中以及下文所有未额外说明的物理量都是已经约去单位的物理量。
边界条件
通常使用周期性边界条件。
也有直接研究有限边界,边上的格点除了和有限点阵中周围其他格点相互左右,还和一个不存在的虚格点作用,这个虚格点的自旋为0或者全部为$+1$(或全部为$-1$)。
算法
小规模二维体系穷举
我们能够确定正确的是直接使用统计力学定义的系综平均来求各个统计量。所以我们先用超小规模的体系标定一组可以作为基准的数据。
在缺乏实验数据和理论解析解的情况下,使用定义求解小体系得到绝对可靠的数据作为基准是确认后续模拟方法正确的必要操作。
体系设定
Benchmark的选择是$5\times5$的体系在$T=1.0$到$T=5.0$下的零外场的性质。由于$2^{25}=33554432\sim 10^7$还是可以直接计算的,所以可以通过Python很快写一个测试,直接产生$2^{25}$个构型,分别计算能量和磁矩。最后在不同温度下按照Boltzmann加权计算平均值即可。这样的值是精确的数值值。注意只需要计算一次所有构型的能量和磁矩,保存下来就可以快速计算其他所有温度下的物理量。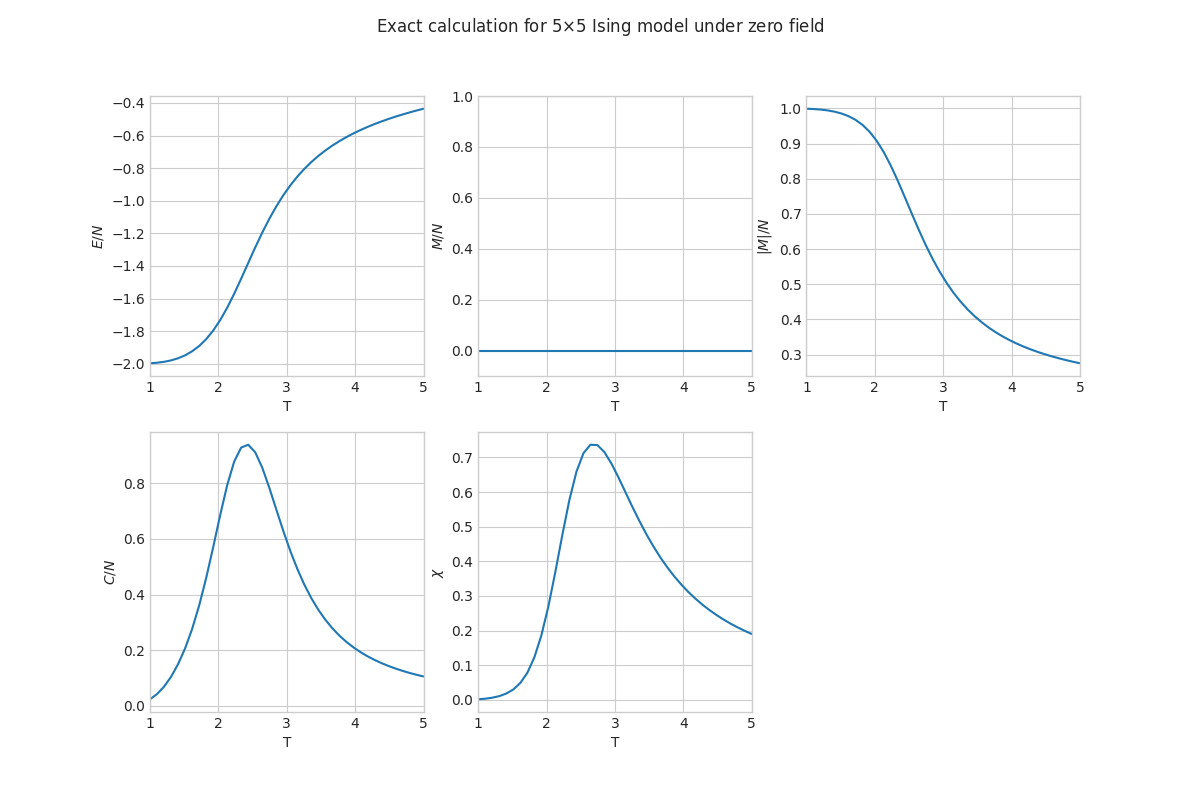
结果分析
首先由二阶矩(热容$C$和磁导率$\chi$)确认在$2<T<3$存在二级相变。然而从图中看到,$5\times5$的体系对于确定精确的临界温度来说还是太小了,尺寸效应使得相变峰不够尖锐。所以,后续实验要确定相变点,就必须增大系统尺寸。
其次,如果直接统计磁矩$m$,发现其值在任意温度下恒为零。这恰好印证了Ising模型的对称性,统计结论是正确的。但是为了观察到有意义的磁矩值,需要改为统计$|m|$。此时可以看到在低温下磁矩趋于1,表示铁磁相,在高温下磁矩趋于零,表示顺磁相。同时$\chi$的统计中需要的磁矩也全部按照$|m|$统计。后面所有的$\chi$也全部按此计算。
Markov Chain Monte Carlo + Metropolis-Hastings
在MC程序中,首先初始化晶格,可以随机生成,也可以选择一个初始构型。因为MC程序原理上可以使体系达到热力学平衡态,所以只要弃掉未平衡的前期数据,只对后边达到平衡的数据做统计,就可以消除初始结构对统计的影响。
MCMC算法中,每一步(flip)循环随机选取一个格点尝试翻转符号,翻转的概率为
$\Delta E$为(假设)翻转后的组态能量减去翻转前的组态能量。
具体的实现可以产生一个满足$[0,1]$上均匀分布的随机数,若小于p值则可以翻转。若大于p值则保持构型不变,对这步不变的构型同样要进行统计(Metropolis算法的要求,满足细致平衡)。
通常,为了使得采样充分,设置一个MC step为$N$个flip,即平均每个格点被尝试翻转一次。每个MC step进行一次统计,求当前构型的各种物理量(能量、磁矩等)。这样运行一次MC程序,跑$Nstep=10^4\sim10^6$个MC step,得到$Nstep$个构型对应的(瞬时)物理量,其中设定达到平衡需要$Ninit$步。之后,对这$Nstep-Ninit$个数据进行统计求均值、方差,就得到统计上的一阶矩(能量、磁矩)和二阶矩(热容、磁化率)等。这算作一次实验。重复进行$n$次实验并作统计,对得到的热力学量求平均和误差,就得到该温度下的全部结果。如果希望提高实验结果精度,减小误差,那么需要增加总的运行步数$n\times Nstep$。如果总运行步数不变,那么统计的精度也不会变。
平衡的判据可以是平均磁矩$m\approx0$。通过观察平均磁矩的变化可以确定平衡步数$Ninit$的大致取值。这个步数不需要特别精确。
以上是最基本的对Ising模型的模拟方法。
Wolff Cluster
当温度接近$T_c$或低于$T_c$时,Metropolis算法非常低效(难以翻越势垒,体现为系统的平均磁矩难以达到零)。Wolff Cluster算法利用Gibbs采样的思想,可以解决这个问题。
Wolff, Ulli. “Collective Monte Carlo updating for spin systems.” Physical Review Letters 62.4 (1989): 361.
每一步循环随机选取一个格点作为起始点加入“团簇”;
检查“团簇”中所有未检查过的点:
查看其所有未加入团簇的最近邻格点,若被检查的最近邻格点与当前格点的符号相同,则按照概率$p=1-\exp(-2\beta J_{ij})$将其加入本次循环的“团簇”;重复检查,直到团簇中没有未检查的格点;
最后将团簇中的所有格点符号翻转。
实现时,显然可以用队列实现团簇的增长和检查。
很有价值的Ising模型计算报告参考
http://physics.bu.edu/~py502/lectures5/mc.pdf
非常详细、深入的二维Ising模型的模拟,随网站提供了代码。对$M$和$|M|$区分得很清楚。对磁化率susceptibility的推导非常清楚(式44)。对有限体系在一切温度都应该用式44,因为在有限高温时$|m|$不为零(图15)。
参考资料
- Christensen, Kim, and Nicholas R. Moloney. Complexity and criticality. Vol. 1. World Scientific Publishing Company, 2005.
- Ising model. Wikipedia (2018.5)
- Cluster Algorithms for the Ising Model. Alex’s Notes (2018.5)
- Pathria, R. K., and P. D. Beale. Statistical mechanics. 2011.
- Ising, Ernst. “Beitrag zur theorie des ferromagnetismus.” Zeitschrift für Physik 31.1 (1925): 253-258.(原始文献,德语)
- Feynman, Richard Phillips, Robert B. Leighton, and Matthew Sands. The Feynman lectures on physics, vol. 2: Mainly electromagnetism and matter. Addison-Wesley, 1979. http://www.feynmanlectures.caltech.edu/II_35.html
- PAC, 1997, 69, 1251 (Glossary of terms used in bioinorganic chemistry (IUPAC Recommendations 1997)) on page 1284
- Baxter, Rodney J. Exactly solved models in statistical mechanics. Elsevier, 2016.
- Chandler, David. Introduction to Modern Statistical Mechanics, Oxford University Press, Sep 1987.