习题解答
这里的解答是我个人参考原solution manual之后的详细答案。其中,第6章后半习题大多为数值模拟,没有包含在解答内。如果对答案有疑问或发现其中的错误,欢迎讨论。
Chandler Stat Mech Solution Manual Chapter 1
Chandler Stat Mech Solution Manual Chapter 2
Chandler Stat Mech Solution Manual Chapter 3
Chandler Stat Mech Solution Manual Chapter 4
Chandler Stat Mech Solution Manual Chapter 5
Chandler Stat Mech Solution Manual Chapter 6
Chandler Stat Mech Solution Manual Chapter 7
Chandler Stat Mech Solution Manual Chapter 8
讨论
Wikipedia中热力学概念、公式合集
Chandler第一章总结,实际上在Wiki上有一页十分完整:Thermodynamic potential。
Wiki中关于热力学公式的合集:Tables of thermodynamic equations
关于热力学基础,必须记住的有:
- 基本的印象,包括熵的定义、绝热过程、可逆过程、等外压过程等。
- 热一+热二得出平衡态的状态方程(EOS)以及Legendre变换得到的另外三个热力学函数和方程。热力学函数对热力学参数的直接偏导关系(单纯通过这些EOS能够直接推出一些偏导,但是还有一些偏导推不出来,需要通过下面的关系式间接推)。
- Maxwell关系,热力学参数之间的偏导关系。还有$\left(\frac{\pd x}{\pd y}\right) _ z=-\left(\frac{\pd x}{\pd z}\right) _ y\left(\frac{\pd z}{\pd y}\right) _ x$当$z=z(x,y)$。
- Gibbs-Duhem方程,给出与EOS补充的微分方程。
- 热力学参数之间的关系往往是系统的特性,例如$p-V-T$关系(等温压缩系数、等压热膨胀系数)、$S-V,p$关系(热容)等。
- $S,T,p,v$知道两个就能确定剩余两个,也就是说一个参数是任意另外两个参数的函数($n$不变时)。
关于熵和温度
Chandler这本书中直接假设熵随能量单增(p10),这样其导数温度就是恒正。我有点觉得这个假设有些不严谨。平衡态热力学中温度为正值是热力学第三定律的直接推论。另外所谓的“负温度”应该不属于平衡态热力学的理论,这个粒子数反转态应该是一个不稳定态。
关于稳定性理论(stability condition)
这个地方各本书似乎都在跳步骤。偶然搜到关于稳定性理论讲得很好的一章,在Callen, Herbert B - Thermodynamics and an Introduction to Thermostatistics 2nd Edition第八章。
其实内容上并无特别不同,只是我觉得Callen的讲法在5秒钟之内让人彻底理解为何会存在这些不等式条件:本质都是热力学第二定律要求的熵函数$S(E,V,n)$的凸性。这样的话就省去了啰嗦的内部约束或者分成两个系统这样的证明过程,所有的性质都是系统单独就具有的。
此外,熵函数对能量的凸性与其单调性(单增减)无直接关系,也就省去了假设温度为正的问题。当然最后推出热容之类的量的限制条件是要用温度为正这一条件的。在平衡态热力学中温度恒为正是热力学第三定律(能斯特热定理)的结论。
水的相图
Chandler第二章提出水的0℃下的pv相图的问题却没有回答。关于水的pv相图,可以直接找p-v-T相图观察: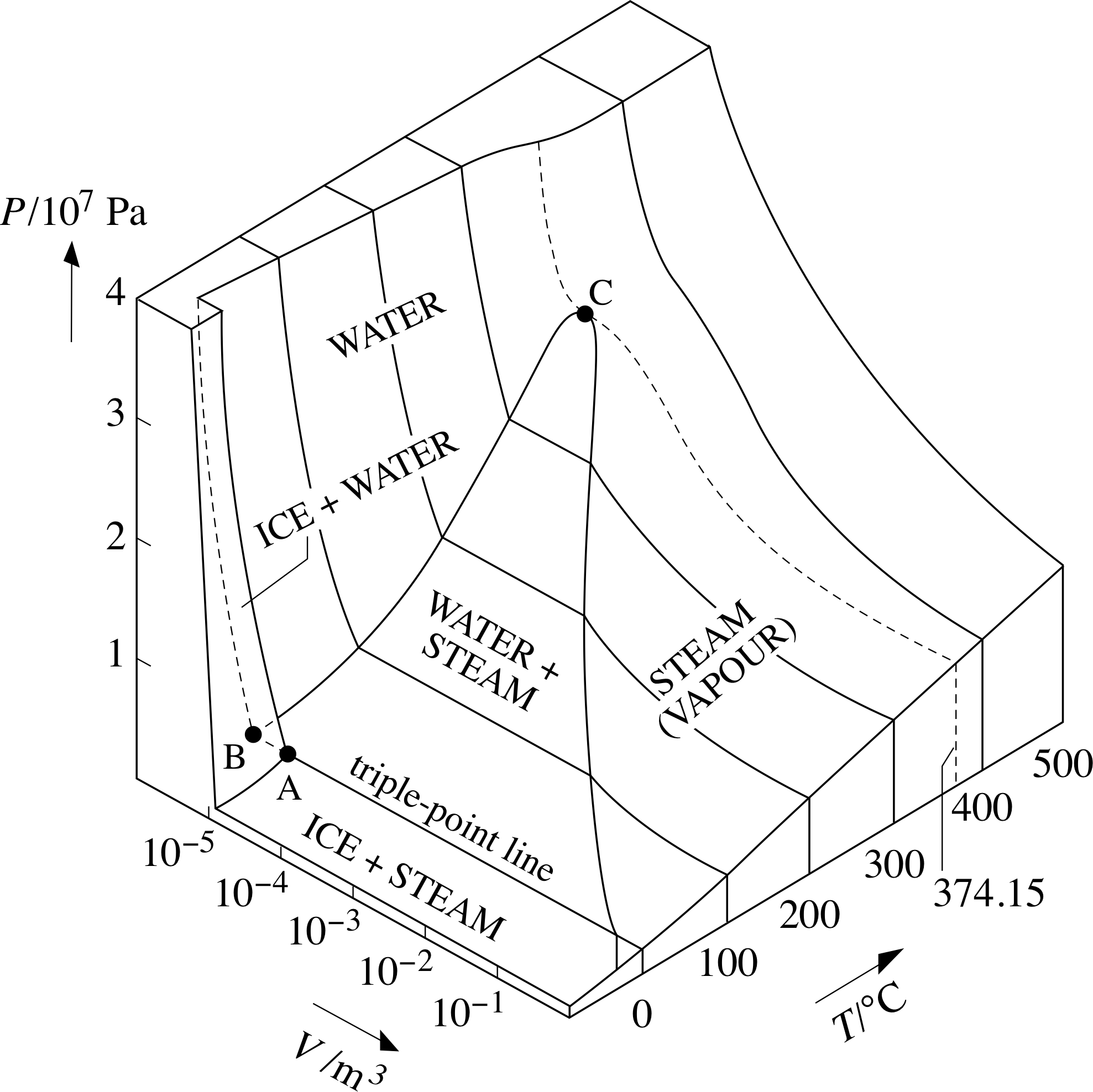
而普通物质的相图如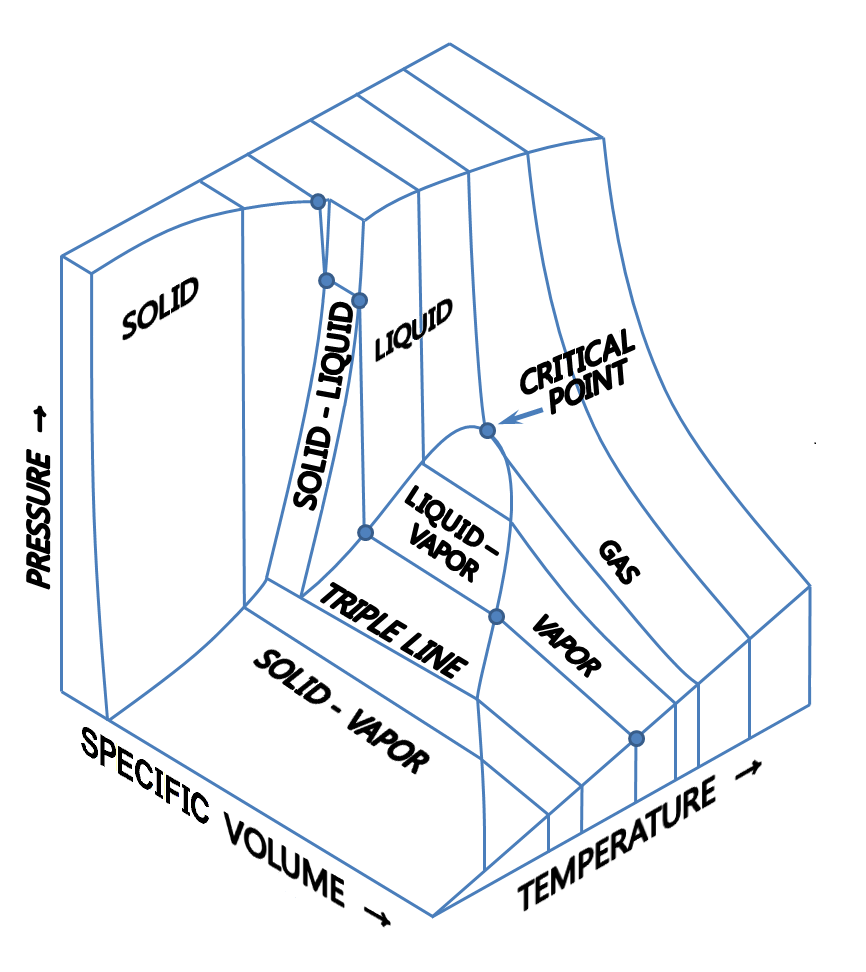
所以原文Fig2.7a是不对的,Fig2.7b是对的。
一篇关于水的相图的模拟的文章:http://pubs.rsc.org/en/content/articlehtml/2009/CP/B812832D
表面张力
习题2.17表达得极其随意——“This means that there will be surface interaction energies with the walls that are also propotional to $\sigma$”这里的walls是什么意思?读了几遍猜想这个能量说的可能是系统内物质与其抽象容器的界面处的属于系统的能量。
经典流体复习总结
半学期过后,之前预习的关于经典流体(Chandler Chapter 7)和非平衡统计(Chapter 8)都忘得差不多了。这里结合Pathria的教材串讲一次作为复习。
Pathria(10.7)直接从关联入手:首先是单粒子数密度的直接定义
$\rho(\br)d\br$就是$d\br$中粒子的个数。其意义从积分可以看出来
注意这个密度的定义是统计上的。接着定义二粒子数密度
$\rho^{(2)}(\br,\br’)d\br d\br’$就是粒子1在$d\br$中、粒子2在$d\br’$中的粒子对12的数目。其积分为
将某一构型的密度函数视为随机变量,定义$X(\br)=\sum_i\delta(\br-\br_i)$,$Y(\br’)=\sum_j\delta(\br’-\br_j)$,其中$\br$和$\br’$表示两个不同粒子的坐标。随机性由构型$\br_i$带来,则$E[X(r)]=\rho(\br)$,$E[Y(r’)]=\rho(\br’)$,
则两个不同的粒子的密度函数之间的协方差,即统计力学中的关联函数Corrlation function为
显然,当两个粒子之间无相互作用时,$\rho^{(2)}(\br,\br’)=\rho(\br)\rho(\br’)$,$C(\rho(\br),\rho(\br’))=0$。
通常的系统(哈密顿量)具有空间平移和旋转不变性,则密度函数与空间坐标无关(空间均匀分布),二阶约化密度函数只与两粒子之间的距离$r=|\br-\br’|$有关。在这个基础上,定义
就是径向分布函数或者称为对关联函数。
之所以称作径向分布函数,是因为$4\pi r^2\rho g(r)dr$表示以某个粒子的坐标为原点,在半径为$r$厚度为$dr$的球壳中的粒子数。这一点可以如此推出:在给定的一个粒子$r$处有粒子的概率用条件概率表示为
Chandler则明确地展示了密度函数、角度分布函数和哈密顿量之间的关系。Chandler的导出如下:一般地,配分函数写为
按照配分函数的统计本质,被积函数实际上联系着该构型的概率。即在$U(\br^N)$相互作用控制下,粒子$1,2,\cdots, N$处于$\br^N=(\br_1,\br_2,\cdots,\br_N)$位置的概率密度为
那么,单个粒子的平均空间密度为
这里$C=\int \br^{N-1}\exp[-\beta U(\br^N)]$。因为空间的平移不变性(Hamiltonian的各项同性),所以被积的指数函数只要$3(N-1)$个自由度就可以确定(不好理解的话举一个二体相互作用的例子),因此$C$与剩余的指标$\br$无关。最后的结果就是粒子密度$\rho$在空间中均匀分布,
按照这个思路,二电子的概率密度分布,即体系中某两个电子处在$\br_1$和$\br_2$的概率
同理,在各向异性Hamiltonian下这个函数实际上只有一个自由度,即$\rho^{(2)}(\br_1,\br_2)=\rho^{(2)}(\br_{12})=\rho^{(2)}(r_{12})$。
实际上途径是一样的。再往下走到径向分布函数和结构因子的关系,交代下和实验的联系,即从实验获得径向分布函数。当然,另一条线是从理论导出,这也是理论重难点。在将理论之前,先说明这个径向分布函数可以给出许多热力学性质,有点类似解配分函数的作用。一个例子是体系能量
这个式子可以由配分函数开始配合二阶约化密度函数的定义导出。其中$u(r)$表示任何两个粒子之间的相互作用,即$U(\br^N)=\sum_i u(r_{ij})$。同时,压强为
这个公式称为virial定理,如果已知对势$u(r)$以及能够通过理论推出$g(r)$,就可以得到一个状态方程。如果只保留第一项1,就回到理想气体状态方程。对积分按密度展开的方法就是virial展开。
Virial展开可以配合可逆功定理:
其中$w(r)$表示在NVT下将系统中两个粒子由无穷远可逆地移动到距离$r$的状态所做的功,即这个过程的Helmholtz自由能差
这个定理实际上有点平均场的感觉。如果将功分为该粒子对的对势的功和其他粒子的场功$w(r)=u(r)+\Delta w(r)$,忽略$\Delta w(r)$,那么virial可以展开到密度的二次项
其中
即为第二virial系数。函数$f(r)$称为Mayer函数。求高阶virial系数的方法称为Mayer Cluster Expansion。
至于理论上已知$u(r)$解$g(r)$或$f(r)$的近似方法,有Scaled-Particle Theory(SPT)以及Percus-Yevick近似。这些Chandler书上没讲,具体可以看文献。